CornerNet

CornerNet: Detecting Objects as Paired Keypoints

1 Introduction

…

在本paper中，我们介绍了CornerNet，这是一种新的单步目标检测方法，可以消除anchor box。我们用一对关键点来检测目标——目标的左上角点和右下角点，我们还使用单个卷积网络来预测同一目标类的所有实例的左上角点的heatmap，右下角点的heatmap，以及每个检测角点的embedding vector。embedding将属于同一目标的一对角点分组——训练网络来为相同目标的角点预测相似的embedding。…。Fig.1阐明了我们方法的基本流程(pipeline)。

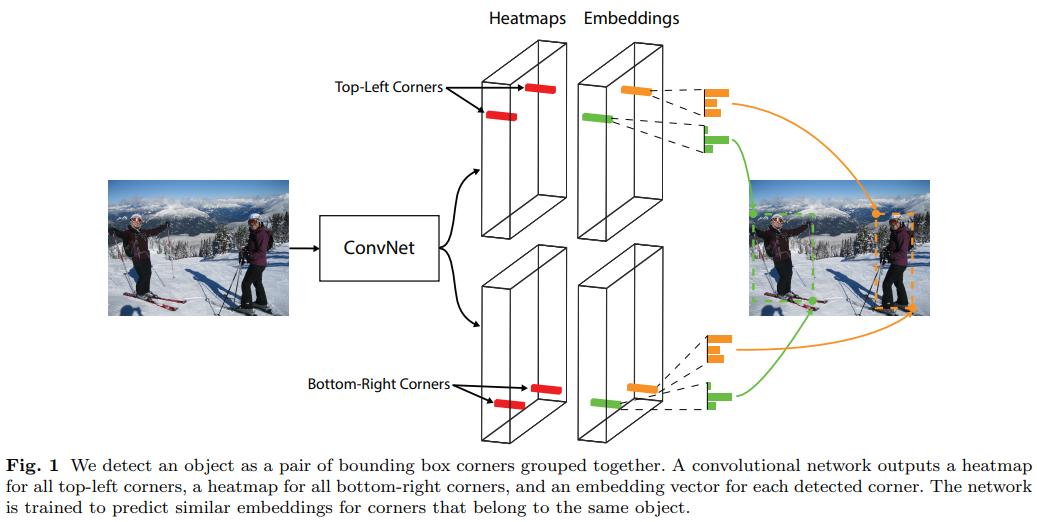
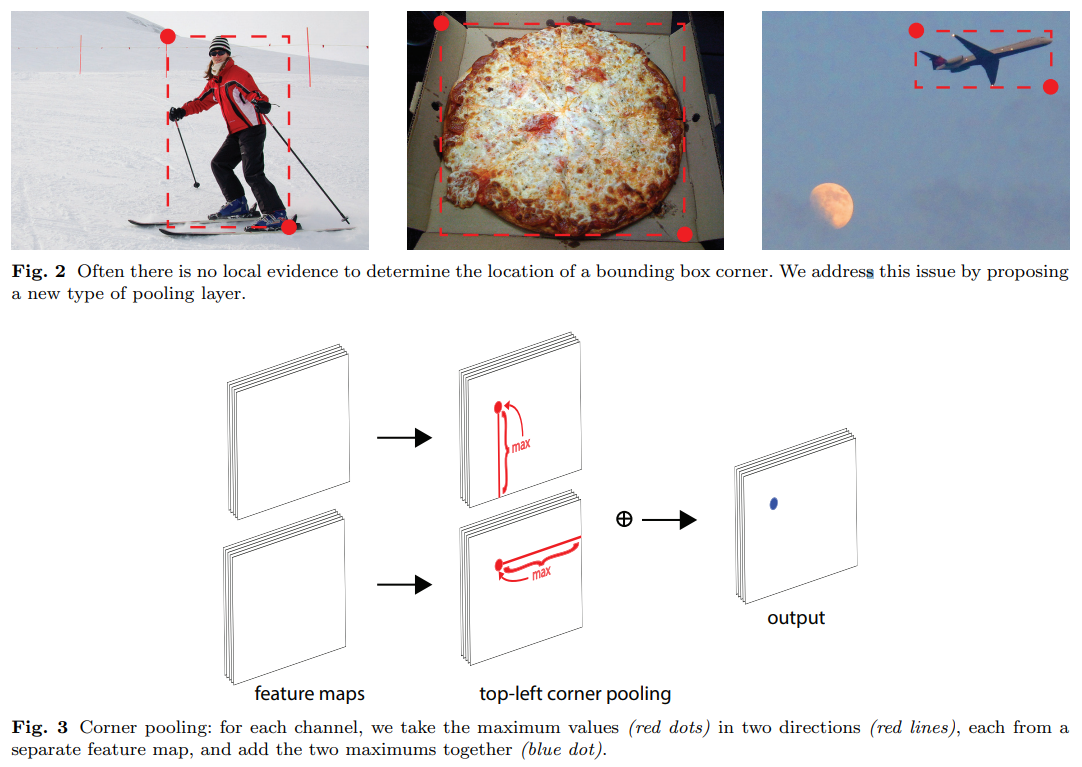
CornerNet的另一创新处是角池化(corner pooling)，一种新的池化方式帮助卷积网络更好的定位边界框的角点。边界框的角点通常在目标之外————考虑一个圆或Fig.2中的例子，在这种情况下角点无法根据局部信息进行定位。取而代之，为了确定像素位置是否为左上角点，我们需要水平向右寻找目标最上边界，并垂直向下寻找最左边界。这激发了我们的角池化层(corner pooling layer)：它接收两个特征图，在每个像素位置它将来自第一个特征图右侧的所有特征向量最大池化，并将来自第二个特征图下方的所有特征向量最大池化，见Fig.3的例子。

水平向右寻找目标最上边界，并垂直向下寻找最左边界???

…

3. CornerNet

3.1 Overview

在CornerNet中，我们用一对关键点来检测目标——目标的左上角点和右下角点。卷积网络预测两组heatmap来表示不同目标类的角点位置，一组表示左上角点一组表示右下角点。网络还为每个检测的角点预测embedding向量，以便使同一目标的两个角点的embedding之间的距离很小。为了产生紧密的边界框，网络还预测offsets以微调角点的位置。根据预测的heatmaps, embeddings and offsets，我们使用了简单的后期处理算法来得到边界框。

heatmap：热视图，可理解为一种特殊的特征图。

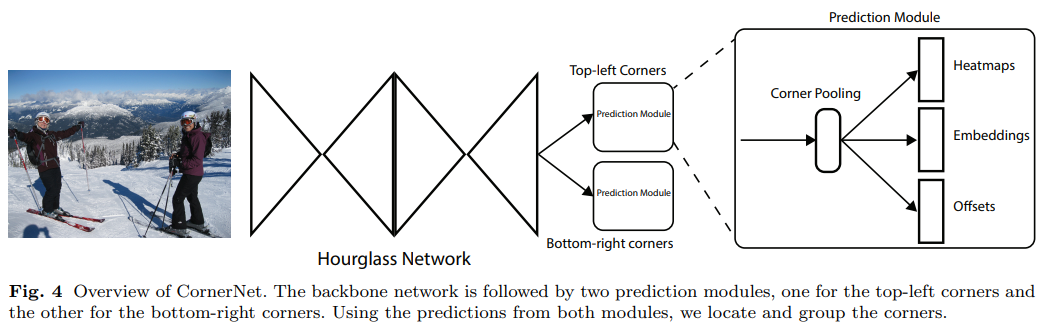
Fig.4提供了CornerNet的概述，我们用hourglass网络作为骨干网络，后接两个预测模块，一个模块预测左上角点，一个模块预测右下角点，每个模块有自己的角池化模块，从而在预测heatmaps, embeddings and offsets之前将来自hourglass网络的特征池化。不像其他的目标检测，我们不使用不同尺度的特征来检测不同大小的目标，我们只将两个模块应用于hourglass网络的输出上。

3.2 Detecting Corners

我们预测两组heatmap，一组用于左上角点一组用于右下角点。每组heatmap有$C$通道和$H\times W$大小，$C$是类别数，没有背景通道，每个通道是一个二进制掩膜(binary mask)，用于指示类的角点位置。

二进制掩膜(binary mask)??

*对于每个角点，有一个gt positive location，其它所有位置均为negitive*。在训练期间，我们并不是平等地惩罚每一个negative location，而是减少了对positive location半径内的negative location的惩罚。这是因为如果一对错误的角点检测与各自的gt位置足够近的话，它们也能产生满足与gt的重叠度的一个框(Fig.5)。我们通过确保半径内的一对点可以生成一个与gt标注的IOU至少为$t$的边界框(我们在所有的实验中将$t$设为0.3)，*进而通过目标大小确定半径*。给定半径，惩罚量的减少由非标准2D高斯给出，$e^{-\frac{x^{2}+y^{2}}{2\sigma^{2}}}$，其中心在positive location，$\sigma$是半径的$¹⁄₃$。

对于每个角点，有一个gt positive location，其它所有位置均为negitive??

令$p_{cij}$为预测heatmap中位置$(i,j)$对于$c$类的分数，令$y_{cij}$为用非标准高斯增强的“gt”的heatmap，我们设计了focal损失的变种：

focal损失

$$ L_{det}=\frac{-1}{N} \sum_{c=1}^{C} \sum_{i=1}^{H} \sum_{j=1}^{W}\left\{\begin{array}{cl} {\left(1-p_{c i j}\right)^{\alpha} \log \left(p_{c i j}\right)} & {\text{if }y_{cij}=1} \
{\left(1-y_{c i j}\right)^{\beta}\left(p_{c i j}\right)^{\alpha} \log \left(1-p_{c i j}\right)} &{\text { otherwise }}\end{array}\right. \tag{1} $$

其中$N$是图像中目标的数量，$\alpha$和$\beta$是控制每个点分布的超参数(我们在所有实验中将$\alpha$设为2，$\beta$设为4)。利用$y_{cij}$中编码的高斯凸起，$(1-y_{cij})$项减少了gt位置附近的惩罚。

许多网络加入了下采样层来收集全局信息并减少内存使用，当它们全卷积应用于图象时，输出大小通常小于图像。因此，图像中的位置$(x,y)$被映射到heatmap中的位置$([\frac{x}{n},\frac{y}{n}])$，其中$n$是下采样因子。当我们将位置从heatmap重映射到输入图像时，可能会丢失一些精度，这会极大影响小边界框和其gt的IOU。为了解决这一问题，我们先预测位置偏移量来微调角点位置，然后将位置重映射到输入尺寸。

$$ \omicron_{k}=(\frac{x_{k}}{n}-[\frac{x_{k}}{n}],\frac{y_{k}}{n}-[\frac{y_{k}}{n}]) \tag{2} $$

其中$\omicron_{k}$是偏移量offsets，$x_{k}$和$y_{k}$是角点$k$的x和y坐标。实际上我们预测由所有类的左上角点共享的一组offsets，和由右下角点共享的另一组offsets。训练时，我们对gt角点位置应用smoothL1损失：

$$ L_{off}=\frac{1}{N}\sum_{k=1}^{N}\text{SmoothL1}(\omicron_{k},\hat{\omicron}_{k}) \tag{3} $$

3.3 Grouping Corners

多个目标可能会出现在同一图像中，因此可能检测到多个左上角点和右下角点。我们需要确定一对左上角点和右下角点是否来自同一个边界框。我们的方法受Newell等人为多人位姿估计任务提出的 Associative Embedding方法的启发，他们检测所有的人类关节并为每一个检测的关节生成一个embedding，根据embedding之间的距离对关节进行分组。

关联的embedding思想同样也适用于我们的任务，网络为每个检测角点预测一个embedding向量，使得如果一个左上角点和一个右下角点属于同一边界框，它们的embedding的距离就应该很小。然后我们基于左上角点和右下角点的embedding之间的距离对角点分组，embedding的实际值并不重要，只有embedding之间的距离被用于对角点分组。

我们根据Newell等人使用1维的embedding。令$e_{t_{k}}$和$e_{b_{k}}$分别为目标$k$的左上角点和右下角点的embedding。和Newell和Deng提到的一样，我们使用“pull”损失训练网络给同一目标的角点分组，使用“push”损失分离不同目标的角点：

$$ L_{pull}=\frac{1}{N} \sum_{k=1}^{N}\left[\left(e_{t_{k}}-e_{k}\right)^{2}+\left(e_{b_{k}}-e_{k}\right)^{2}\right], \tag{4} $$

$$ L_{push}=\frac{1}{N(N-1)} \sum_{k=1}^{N} \sum_{j=1 \atop j \neq k}^{N} \max \left(0, \Delta-\left|e_{k}-e_{j}\right|\right), \tag{5} $$

其中$e_{k}$是$e_{t_{k}}$和$e_{b_{k}}$的均值，我们在所有的实验中设$\Delta=1$。和偏移的损失相似，我们只在gt角点位置应用损失。

3.4 Corner Pooling

如Fig.2所示，通常没有角点存在的局部视觉证据。为了确定一个像素点是否为左上角点，我们需要水平向右寻找目标最上边界，并垂直向下寻找最左边界，因此我们提出角池化(corner pooling)通过编码显式先验知识以更好地定位角点。

假设我们想要确定位置$(i,j)$的像素是否为左上角点，令$f_{t}$和$f_{l}$为左上角点池化层输入的特征图，令$f_{t_{ij}}$和$f_{l_{ij}}$分别为$f_{t}$和$f_{l}$位置$(i,j)$处的向量。角池化层首先将$f_{t}$中$(i,j)$和$(i,H)$之间所有特征向量最大池化得到一个特征向量$t_{ij}$，并将$f_{l}$中$(i,j)$和$(W,j)$之间所有特征向量最大池化得到一个特征向量$l_{ij}$。最后将$t_{ij}$和$l_{ij}$相加，该计算可由下面公式表达：

$$ t_{i j}=\left\{\begin{array}{cl}{\max \left(f_{t_{i j}}, t_{(i+1) j}\right)} & {\text { if } i<H} \\ {f_{t_{H j}}} & {\text { otherwise }}\end{array}\right. \tag{6} $$

$$ t_{i j}=\left\{\begin{array}{cl}{\max \left(f_{l_{i j}}, l_{(i+1) j}\right)} & {\text { if } j<W} \\ {f_{l_{i W}}} & {\text { otherwise }}\end{array}\right. \tag{7} $$

其中我们应用了元素最大值操作，$t_{ij}$和$l_{ij}$都可以通过动态编程(Fig.6)有效计算。

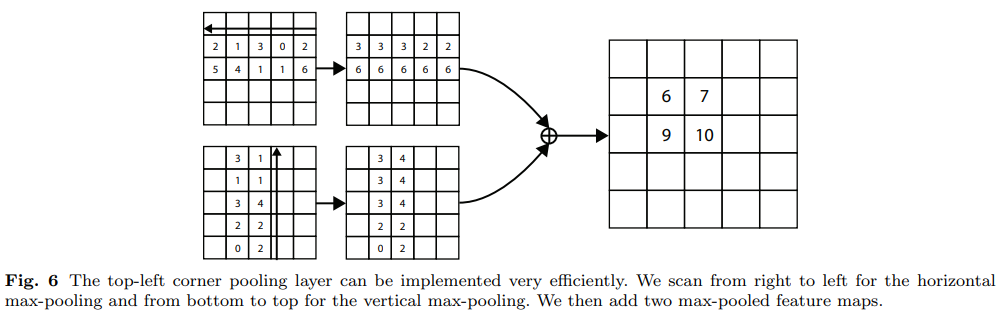
我们以相似的方式定义了右下角池化层，它最大池化$(0,j)$和$(i,j)$之间所有特征向量和$(i,0)$和$(i,j)$之间所有特征向量，然后将这些池化结果相加。角池化层在预测模块中使用以预测heatmaps, embeddings and offsets.

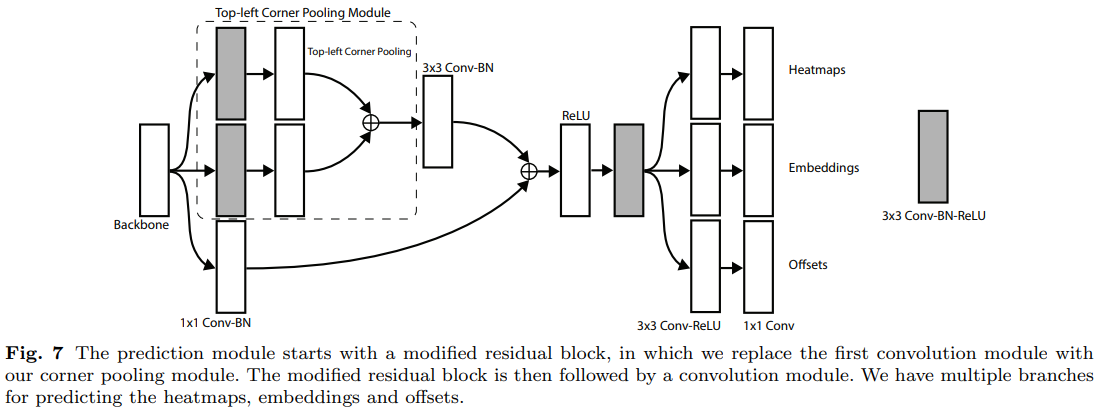
预测模块的架构见Fig.7，模块的第一部分是残差块的修改版，在这修改的残差块中，我们将第一个$3\times3$的卷积模块替换为角池化模块，它首先用两个有128通道数的$3\times3$的卷积模块处理来自骨干网络的特征，然后应用角池化层。根据残差块的设计，我们将池化的特征投入有256通道数的$3\times3$的Conv-BN层，然后与投影shortcut相加。修改的残差块后接一个有256通道数的$3\times3$的卷积模块，以及3个Conv-ReLU-Conv层，以产生heatmaps, embeddings and offsets.

3.5 Hourglass Network

CornerNet使用hourglass网络作为其骨干网络，hourglass网络首先用于人体姿态评估任务。它是包含一个或多个hourglass模块的全卷积网络，一个hourglass模块首先用一系列卷积和最大池化层将输入特征下采样，然后用一系列上采样和卷积层将特征上采样到原始分辨率。由于信息细节在最大池化层丢失了，所以添加skip layer将细节带回上采样的特征。hourglass模块在单个统一架构中同时捕获全局和局部特征，当多个hourglass模块在网络中堆叠(stack)时，hourglass模块可以重复处理特征以捕获更高级的信息。这些属性使hourglass网络也成为目标检测的理想选择，事实上，目前许多检测器已经采用了和hourglass相似的网络。

我们的hourglass网络包含两个hourglass模块，我对其架构做了一些修改，简单使用步长2来降低特征分辨率而不是使用最大池化。我们将特征分辨率降低了5次，并在此过程中增加了特征通道数(256,384,384,384,512)。当我们上采样特征时，我们应用2个残差模块，后接一个最邻近上采样(nearest neighbor upsampling)。每个skip connection也包含2个残差模块，在一个hourglass模块中有4个512通道数的残差模块。在hourglass模块前，我们将图像分辨率降低了4倍，使用了步长为2通道数为128的$7\times7$卷积模块后接步长为2通道数为256的残差块。

根据Newell等人的工作，我们还在训练时增加了中间监督(intermediate supervision)，然而，我们并没有将中间预测加入网络，因为我们发现这会影响网络性能。我们将$1\times1$的Conv-BN模块同时应用到第一个hourglass模块的输入和输出，然后逐元素相加合并它们，后接一个ReLU和通道数为256的残差块，然后被作为第二个hourglass模块的输入。hourglass网络的深度达104，不像其它的前沿检测器，我们只使用来自整个网络最后一层的特征进行预测。

4 Experiments

4.1 Training Details

我们在PyTorch上实现了CornerNet，网络由PyTorch的默认设置初始化，没有在任何外部数据集上预训练。在应用focal损失时，我们根据Lin等人来设置用于预测角点heatmap的卷积层的偏向值。在训练期间，我们将输入分辨率设为$511\times511$，因此输出分辨率为$128\times128$。为了减少过拟合，我们采用标准数据增强技术，包括随机水平翻转，随机缩放，随机裁剪，随机颜色抖动(包括调整图像亮度，饱和度，对比度)。最后，我们在输入图像上应用PCA。

PCA(PrincipalComponents Analysis)即主成分分析，是图像处理中经常用到的降维方法 了解截断SVD

我们使用Adam优化整个训练损失：

$$ L=L_{det}+\alpha L_{pull}+\beta L_{push}+\gamma L_{off} \tag{8} $$

其中$\alpha,\beta,\gamma$是各损失的权重，我们令$\alpha=\beta=0.1,\gamma=1$，我们发现$\alpha$和$\beta$取1或更大值时会导致较弱的性能。我们使用的batch大小为49并在10个Titan X上训练(主GPU4张图，其余各GPU5张图)，为了节约GPU的资源，在我们的消融测试中，我们将网络用$2.5\times10^{-4}$的学习率训练了250k个迭代次数，将其结果与其它检测器比较时，我们将网络额外训练了250k个迭代次数，并把学习率降低为$2.5\times10^{-5}$最后训练了50k个迭代次数。

4.2 Testing Details

在测试时，我们使用了简单的后期处理算法通过heatmaps,embeddings and offsets生成边界框。我们首先通过在角点heatmap上使用$3\times3$最大池化层应用NMS，然后从heatmap上挑选前100个左上角点和前100个右下角点，角点位置通过相应的offsets得到调整，我们计算了左上角点和右下角点的embedding的L1距离，拒绝了距离超过0.5或包含不同类角点的一对角点，左上角点和右下角点的平均分数被用作检测分数。

我们保持图像的原始分辨率，在投入CornerNet前用零进行padding操作，而不是调整图像到固定大小。原图和翻转的图像都用于测试，我们结合了原始图像和翻转图像的检测结果，并应用soft-nms来抑制多余检测，只报告前100个检测结果。平均检测时间在Titan X上是每张图244ms。

4.3 MS COCO

…