MobileNet

MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications

1. Introduction

…

本paper描述了一个高效的网络架构和一组双超参数(a set of two hyper-parameters)，以构建非常小的，低延迟的模型，这些模型可以轻松地与移动和嵌入式视觉应用的设计要求匹配。

…

2. Prior Work

…

3. MobileNet Architecture

本节我们首先描述建立MobileNet基于的核心层，它们是深度可分离的过滤器。然后描述MobileNet的网络架构，并以两个模型缩减超参数的宽度乘数和分辨率乘数的描述作为结束。

3.1. Depthwise Separable Convolution 深度可分离卷积

MobileNet模型基于的深度可分离卷积是分解卷积的一种形式，它将标准卷积分解为深度卷积(depthwise convolution)和称为点向卷积(pointwise convolution)的$1\times1$卷积。对于MobileNet，深度卷积对每个输入通道应用单个过滤器，然后点向卷积应用$1\times1$卷积合并深度卷积的输出。一个标准卷积在一个阶段同时过滤和组合输入得到一组输出，深度可分离卷积将其拆分为两层，用于过滤的单独层和用于组合的单独层。这种分解何以显著减少计算量和模型大小。Fig.2显示了标准卷积(2(a))是怎么分解为深度卷积(2(b))和点向卷积(2©)的。

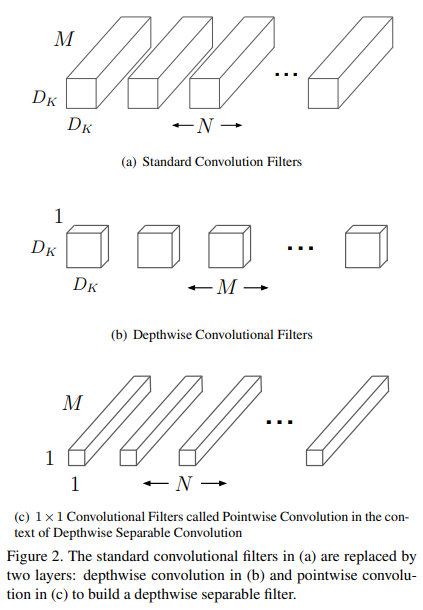
标准卷积层取$D_{F}\times D_{F}\times M$特征图$\mathbf{F}$作为输入，并生成$D_{G}\times D_{G}\times N$特征图$\mathbf{G}$，其中$D_{F}$是方形输入特征图的宽和高，$M$是输入通道数(输入深度)，$D_{G}$是方形输出特征图的宽和高，$N$是输出通道数(输出深度)。

标准卷积层由大小为$D_{K}\times D_{K}\times M\times N$的卷积核$\mathbf{K}$参数化，其中$D_{K}$是卷积核(假定为方形)的空间维度。

假定步长为1且有padding标准卷积的输出特征图计算方式为：

$$ \mathbf{G}_{k,l,n}=\sum_{i,j,m} \mathbf{K}_{i,j,m,n} \cdot \mathbf{F}_{k+i-1,l+j-1,m} \tag{1} $$

标准卷积的计算成本为：

$$ D_{K} \cdot D_{K} \cdot M \cdot N \cdot D_{F} \cdot D_{F} \tag{2} $$

MobileNet模型解决了计算成本中的每一个因素及其相互作用，它首先使用深度可分离卷积打破了输出通道数和卷积核大小的相互作用。

标准卷积运算具有基于卷积核过滤特征并组合特征以产生新表示的效果，过滤和组合可通过叫做深度可分离卷积的分解卷积拆分为两步，以降低计算成本。

深度可分离卷积包括两层：深度卷积和点向卷积。我们使用深度卷积以在每个输入通道(输入深度)上应用单个过滤器，然后点向卷积，也就是$1\times1$卷积，被用于创建一个深度层输出的线性组合。MobileNet对两个层都使用BN和ReLU非线性。

深度卷积可被写为：

$$ \hat{\mathbf{G}}_{k,l,m}=\sum_{i,j} \hat{\mathbf{K}}_{i,j,m} \cdot \mathbf{F}_{k+i-1,l+j-1,m} \tag{3} $$

其中$\hat{\mathbf{K}}$是深度卷积核，$\hat{\mathbf{K}}$中第$m$个过滤器被应用于$\mathbf{F}$中第$m$个通道，以产生输出特征图$\hat{\mathbf{G}}$的第$m$个通道。

深度卷积的计算成本为：

$$ D_{K} \cdot D_{K} \cdot M \cdot D_{F} \cdot D_{F} \tag{4} $$

相对于标准卷积，深度卷积非常有效。但它仅过滤输入通道，不会将它们组合以创造新特征。因此，需要用于计算深度卷积输出的线性组合的额外层($1\times1$卷积)来生成这些新特征。

深度卷积和点向卷积的组合被称为深度可分离卷积。

深度可分离卷积的计算成本：

$$ D_{K} \cdot D_{K} \cdot M \cdot D_{F} \cdot D_{F} + M \cdot N \cdot D_{F} \cdot D_{F} \tag{5} $$

通过将卷积表示为过滤和组合的两步过程，我们可以减少的计算成本：

$$ \begin{aligned} &\frac{D_{K} \cdot D_{K} \cdot M \cdot D_{F} \cdot D_{F} + M \cdot N \cdot D_{F} \cdot D_{F}}{D_{K} \cdot D_{K} \cdot M \cdot D_{F} \cdot D_{F}} \
= &\frac{1}{N}+\frac{1}{D_{K}^{2}} \end{aligned} $$

MobileNet使用$3\times3$的深度可分离卷积，它将计算量减少了8到9倍，而准确度只有小幅下降，详见第4节。

…

3.2. Network Structure and Training

除了第一层的全卷积，MobileNet结构建立于前一节提到的深度可分离卷积。通过以这种简单的方式定义网络，我们能够轻松探索网络拓扑以找到一个好的网络。网络架构定义见Table.1。除了最后的全连接层后面没有ReLU非线性而是投入一个用于分类的softmax层，所有层后面都接有BN和ReLU非线性。Fig.3对比了具有常规卷积，BN和ReLU非线性的层和具有深度卷积，点向卷积，以及每一层后面的BN和ReLU的分解层。下采样是通过在深度卷积以及第一层中的跨步长卷积(strided convolution)处理的。最终的平均池化在全连接层之前将空间分辨率降为1。将深度和点向卷积作为单独的层，则MobileNet有28层。

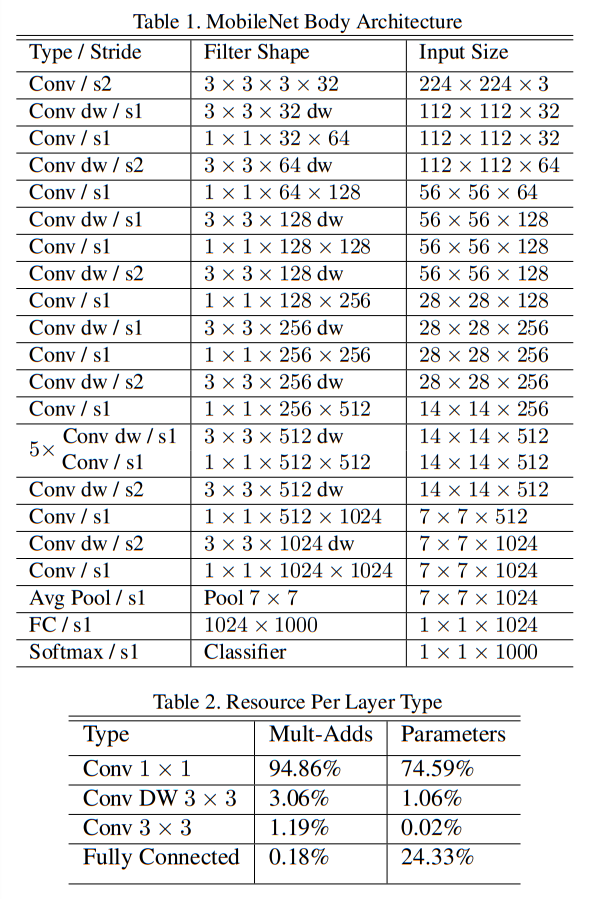
仅用少量的Mult-Adds简单地定义网络是不够的，确保这些运算可以高效执行也很重要。比如非结构化稀疏矩阵运算通常不会比密集矩阵运算快，除非非常高的稀疏度。我们的模型结构将几乎所有计算都放入密集的$1\times1$卷积中。这可以通过高度优化的通用矩阵乘法(GEMM, general matrix multiply)函数来实现。卷积通常由GEMM实现，但需要在内存中进行名为im2col的初始重排序才能将其映射到GEMM。例如，在流行的Caffe软件包中使用了这种方法。$1\times1$卷积不需要在内存中重排序就能通过GEMM直接执行，而GEMM是最优的数值线性代数算法之一。MobileNet将其95%的计算时间花费在$1\times1$卷积中，其中包含75%的参数，见Table.2。其余所有参数几乎都在全卷积层中。

MobileNet模型是在TensorFlow中使用RMSprop进行训练的，并具有类似于InceptionV3的异步梯度下降(asynchronous gradient descent)。但是，与训练大型模型相反，我们使用较少的正则化和数据增强技术，因为小型模型的过拟合麻烦较小。在训练MobileNet时，我们不使用side heads或标签平滑，而是另外通过限制small crops(在大型的Inception训练中使用过)的大小减少失真的图像。另外，我们发现对深度过滤器进行很少或几乎没有权重衰减(L2正则化)是很重要的，因为它们中的参数太少了。对于下一节中的ImageNet基准，无论模型的大小如何，所有模型都使用相同的训练参数进行训练。

3.3. Width Multiplier: Thinner Models 宽度乘数

虽然基本的MobileNet架构已经很小且延迟低，很多时候，特定的用例或应用程序可能要求模型更小，更快。为了构造这些较小且计算量较小的模型，我们引入了一个非常简单的参数$\alpha$，称为宽度乘数，其作用就是使每一层均匀变薄。对于给定的层和宽度乘数$\alpha$，输入通道数$M$变成$\alpha M$，输出通道数$N$变成$\alpha N$。

带有宽度乘数$\alpha$的深度可分离卷积的计算成本为：

$$ D_{K} \cdot D_{K} \cdot \alpha M \cdot D_{F} \cdot D_{F} + \alpha M \cdot \alpha N \cdot D_{F} \cdot D_{F} \tag{6} $$

其中$\alpha \in (0,1]$，通常设置为1，0.75，0.5和0.25。$\alpha=1$是baseline MobileNet，$\alpha<1$是reduced MobileNet。宽度乘数的作用是将计算量和参数数量大约减少$\alpha^{2}$倍，从而降低了计算成本。宽度乘数可以应用于任何模型结构，以合理的精度，延迟和大小的权衡来定义新的较小模型。它用于定义新的精简结构，需要从头开始进行训练。

3.4. Resolution Multiplier: Reduced Representation 分辨率乘数

减少神经网络计算成本的第二个超参数是分辨率乘数$\rho$，我们将其应用于输入图像，每一层的内部表示随之以相同的乘数降低。实际上，我们通过设置输入分辨率来隐式设置$\rho$。

现在，我们可以将网络核心层的计算成本表示为具有宽度乘数$\alpha$和分辨率乘数$\rho$的深度可分离卷积：

$$ D_{K} \cdot D_{K} \cdot \alpha M \cdot \rho D_{F} \cdot \rho D_{F} + \alpha M \cdot \alpha N \cdot \rho D_{F} \cdot \rho D_{F} \tag{7} $$

其中$\rho \in (0,1]$，通常隐式设定以使得网络的输入分辨率为224，192，160或128。$\rho=1$是baseline MobileNet，$\rho<1$是reduced computation MobileNet。分辨率乘数的作用是将计算成本降低$\rho^{2}$。

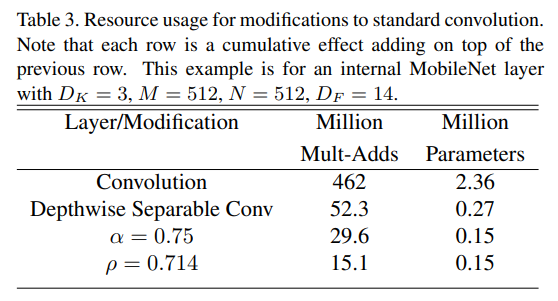
作为示例，我们可以查看MobileNet中的典型层，并了解深度可分离卷积，宽度乘数和分辨率乘数如何减少成本和参数。Table.3显示了将体系结构缩减方法依次应用于该层时该层的计算和参数数量，第一行显示了全卷积层的Mult-Adds和参数，其输入特征图的大小为$14\times 14\times 512$，内核$K$的大小为$3\times 3\times 512\times 512$。我们将在下一节中详细介绍在资源和准确性之间的权衡。

4. Experiments

…